Abstract: Productive learning in the educational environment requires students to participate in consciously active creative process that stimulates mental activities. Problematic situations are often referred to as one of the most optimal means to achieve this goal. The process of resolving problem situations in math is characterized by a set of activities that make up the system of mental and practical operations as hypothesized prominent place.

Key words: problem mathematical problem situation, a situation of speculation

 

Съвремието се побира в рамките на едно модерно хилядолетие, в което обществено-социалната среда се развива и разширява своите изисквания към отделния индивид, а училището отдавна е надхвърлило ролята си на информационно хранилище. Днес съществуват множество източници на знание, които излизат далеч от класната стая. Те налагат една от основните функции на образователния процес, даването на информация, да се измени в тълкуване на вече получена, но неясна такава. Това изисква възникването на нов тип съвременно обучение, което да развива менталния потенциал на учениците посредством огромния поток от знания.

Когато се говори за съвременно обучение става въпрос за развиваща, креативна и в голяма степен мисловна учебно-възпитателна дейност, която да създава не консуматорски, а градивни, творчески личности. От тук се поражда тенденция  за промяна, непосредствено поднесените, готови, знанията да започнат да се усвояват самостоятелно, по евристичен път.

Математическо обучение вече не е насочено единствено към овладяване на определени ситуации от математически тип, то се стреми да научи учениците да прилагат овладените математически знания във всякакви житейски ситуации. Осъществяването на тази цел се постига чрез предлагането и решаването на проблемни ситуации.

Преведени на езика на математиката проблемните ситуации се превръщат в математически проблеми или още в математически проблемни задачи. В обучението по математика в началните класове голяма част от задачите се решават върху основата на вече изучени правила. Значението на тези стандартни правила се състои в това, че те ориентират ученика в отношенията между обектите, чрез които ще се намери решението. Ако е известно какви връзки са необходими при решаването на конкретна задача, това не води до ново откритие. Процесът е алгоритмизиран и води до бързо и точно намиране на отговора. Проблемните ситуации предотвъртяват този процес и принуждават учениците да използват научените правила в непознати и  нетипични ситуации.  С помощта на съвкупност от методи проблемните ситуации се решават, което позволява да се разгърне пълният потенциал на математическото знание като се овладеят  психологията и технологията на  прилагане на информация от математически тип в различни по вид ситуации.

Решаването на проблеми, което се използва в математическата образователна дейност се отнася до процес, при който учениците се сблъскват с проблем- въпрос на който не могат веднага да отговорят или за решаването , на който да приложат готов алгоритъм. Ето защо те трябва да прочетат проблема внимателно, да анализират дадената информация и да изследват  собствените си  математически знания, за да видят могат ли да изградят стратегия, която ще им помогне да намерят решението на съответния проблем. Процесът изисква реорганизация на съществуващите идеи и появата на нови в процеса на работа на учениците.

За разрешаването на една проблемна ситуация ключово значение има откриването на новото,неизвестното.

В.Окон смята, че достигането до проблема или разбирането на проблем, поставен от друг,е изходен пункт за процеса на самостоятелно мислене. Разбира се проблемът трябва да е добре подбран и свързан с потребностите на индивида, така че у него да се породи желание за разрешаването му.

Според М.Махмутов постановката на проблема включва анализ на проблемната ситуация,осъзнаване същността на затруднението, словесно формулиране на проблема.

Проследявайки решаването на проблема Б.Минчев обръща внимание, че във формулираният проблем в значителна степен се съдържа посоката и възможното качество на решението.

По въпроса за решаване на проблемни ситуации в учебно-възпитателна среда работят редица автори. Много от тях създават общи модел за решаване, характеризиращи се с определени етапи. Пример за общо решаване на проблеми е  моделът на  Дж. Брансфор ИДЕАЛ:

1. Идентифициране на проблема.
2. Дефиниране на проблема.
3. Експедиране на проблема от различни гледни точки.
4. Анализиране на възможните стратегии на решаване и тяхното прилагане.
5. Ликвидация на съмненията относно получения отговор чрез проверка.

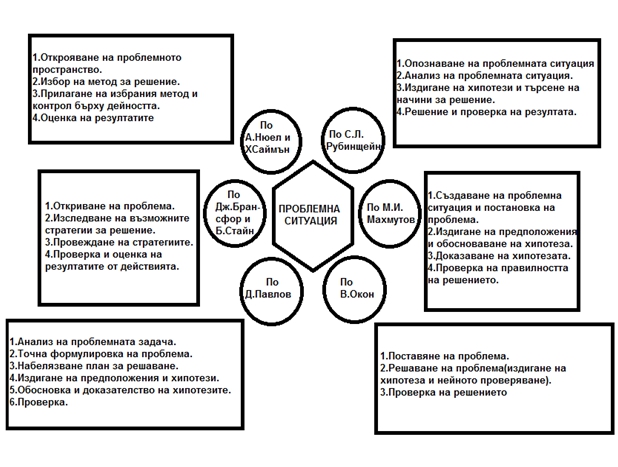
Този модел за решаване на проблеми е с обобщаващ характер и може да се прилага при решаването на всякакъв вид математически проблеми. Подобни модели създават Д.Павлов, В.Окон, М.Махмутов, Х.Саймън и др. ( фиг. 1)

Най-често употребяваният модел за решаване на дидактически проблемни ситуации в обучението по математика е този на Матюшкин.  Процесът на решаване на проблемни задачи Матюшкин разделя на четири етапа:

1. Преобразуване условието на задачата.

Процесът на решаване на една проблемна задача започва с преобразуването на нейното условие. С тази дейност ученикът цели  извършване на  анализ на задачата като актуализира всичките си налични знания,  които биха му помогнали да достигне до решението. По време на анализиране на проблемната задача решаващия я разкрива, че новите условия на действие изискват и нови методи за работа. Този първи етап позволява на учениците да се ориентират в собствените си възможности. Преобразувайки проблемната задача те разбират, че се нуждаят не просто от допълнителни знания,  но и от различни методи и подход към решението.

В следствие от дейността извършена през първия етап се открояват нови връзки и отношения между елементите в задачата, които не са посочени в условието. Този етап може да се определи като „закрито” решаване на проблема т.е. той не се повлиява от външни въздействия.

1. Етап на зараждане на хипотези.

Вторият етап от решаването на проблемната задача е свързан с издигането на хипотетични решения на проблема. Той за разлика от първия етап е „отворен”, което означава че решаващия задачата търси външни условия като далечни връзки, които по-рано са нямали пряко отношение към задачата. През този етап се появява необходимост от преструктуриране на проблема и използването на нови методи на решение, които да доведат до отговора. След преструктурирането на проблемната задача се появяват възможности за поставяне на хипотези, относно нейното решение, които до голяма степен да се доближават до търсения отговор.

2. Реализиране на хипотезите и решаване на задачата.

Реализирането на третия етап се осъществява чрез използването на някои операции за създаването на структури, чрез извършване на изчисления или построяването на система от доказателства, потвърждаващи хипотезата.

3. Проверка на решението.

За да се определи една проблемна задача като решена е необходимо това решение да се провери. Понякога истинността на решението се вижда още в процеса на доказване на поставената хипотеза, но в други случаи изисква специални методи за проверка. В някои случаи дори е възможно и провеждането на експеримент, за да се верифицира решението.

Както се вижда, от посочените модели, изграждането на хипотези е един от ключовите етапи в процеса на решаване на проблемни ситуации. Това дава основание издигането на предположения или още изграждането на хипотези да се определи като процес на хипотезиране.

За решаването на една или друга проблемна ситуация с математически характер е необходимо оптимално съчетание на процесуални и когнитивни умения.

Когнитивните умения, които се включват в решаването на проблеми са:

• Разбиране на стратегиите;
• Създаване на хипотези;
• Предвиждане на резултата, който трябва да се получи;
• Верифициране на хипотетичния резултат и достигане до правилния отговор.

Хипотезирането в случая се явява ключово умение, което насочва решаващия към избора на подходяща стратегия.

Процесът на съставяне на целенасочени предположения за фалсифицируемостта или верифицируемостта на съвкупност от данни и отношения се определя като хипотезиране. То цели откриването на междинни звена, които да хармонират по-далечната цел на математическата проблемна ситуация с наличните средства. Казано с прости думи хипотезирането представлява пътя от догадката до убеждението, то е акт на изграждане на прогнози и целеполагане.

Като краен продукт на дейността хипотезиране се определя хипотезата. Тя се основава на факти и съществува до момента, в който налице е противоречие. Хипотезата е средство за придобиване на нови знания под формата на теоретични конструкции, тя е съчетание от общонаучни и конкретни взаимодействия.

Хипотезата според С. Рубинщайн възниква, когато пред мисълта се постави въпрос, който възобновява изходната проблема. Р. Удуорт определя хипотезата като общо предположение, издигнато под формата на догадка, която подлежи на верифициране. П. Фрес свързва хипотезата с творческия процес, той я характеризира като творческа фаза на експерименталното мислене, чрез която изследователят си представя отношенията, които може да съществуват между обектите. И. Сидоренко дефинира хипотезата като форма на научно познание, което се основава на вероятностите за явления и процеси на основата на наличното у ученика научно познание. М. Мотко смята, че хипотезата задава направлението за осмислено изучаване на обектите. Тя може да се възприеме като форма на регулаторна система, регулираща когнитивната и практическа дейност.

Основната функция на хипотезата се състои в това, че навежда към нови наблюдения.

Водещите процеси, които влияят върху процеса на съставянето на една или друга хипотеза са антиципацията (А) и самоконтролът (К). Съотношението между тях определя как ще бъде изградена съответната хипотеза и доколко тя ще бъде ефективна. Ю. Н. Колюткин предлага следните примери.

Когато А > К решенията се взимат импулсивно. Изградените хипотези в случаите, когато процесите на антиципация преобладават над тези за самоконтрол са съставени набързо без пълно ориентиране в проблемното пространство на задачата.

В случаите, когато антиципацията е по-голяма или равна на самоконтрола се взимат рискови решения, хипотезите са изградени бързо като ориентирането в проблемното пространство е недостатъчно. Въпреки това в процеса на търсене се проявява известен самоконтрол, който ограничава броя на грешните хипотези.

Много рядко се случва процесите на антиципация и самоконтрол да бъдат уравновесени А = К. В тези случаи ориентирането в проблемното пространство на задачата е пълно и изградените хипотези са с висок процент на ефективност.

Възможно е процесите на самоконтрол да бъдат по-големи или равни по количество с тези на антиципация. Решенията в тези случаи се взимат предпазливо. Ориентирането в проблемното пространство е подробно, а хипотезите се изграждат само след внимателна  преценка на различните възможности.

Случва се самоконтролът да преобладава значително над процесите на антиципация К > А, тогава се вземат инертни решения. Хипотезите се построяват неуверено, не поради липса на добра ориентация, а защото ученикът не може да се спре на определена хипотеза.

Процесът на изграждане на хипотези според В.И. Добренков и А.И. Кравченко предлага предвиждане на максимално възможното количество следствия, които произтичат от взаимодействието на обектите.

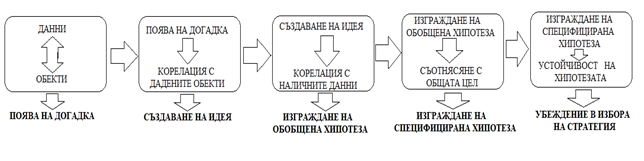
Хипотезирането е сложен акт на прогнозиране на бъдещи състояния на обектите, който преминава през няколко етапа.(фиг.2)

1. Поява на догадка.

В случаите на възникване на проблемна ситуация от математически тип решаващият я преобразува в математическа проблемна задача. Той прочита задачата и у него се заражда неопределено усещане за възможните пътища за решение. Догадката се  основава на противоречието между наличната информация, съвкупност от обекти и данни, и невъзможността ученикът да реши задачата бързо с познати вече средства. Основната цел на догадката е установяване характера на определен обект и връзката му с другите обекти.

2. Създаване на идея.

Идеята представлява основа за извода. Тя изисква от наличното да се премине към нещо отсъстващо. До голяма степен идеята е спекулативна. Нейният извод отива отвъд очевидното за момента, а това налага скок, чиято правилност не може да се гарантира. Създаването на идея изисква от една страна изграждането на съвкупност от инициативност и предпазливост на ума, а от друга подреждане на конкретни факти и обекти, от които произтича.

3. Изграждане на обобщена хипотеза.

Предполагаемият извод от идеята представлява обобщена хипотеза. Тя е опит да се предвидят следващите ходове в процеса на решаване, основани предимно на взаимоотношенията, в които се намират обектите, основни и допълнителни. Обобщената хипотеза е ориентировъчна, когато се корелира с наличните данни и свърже тези данни в система с наличните обекти от обща тази хипотеза се превръща в конкретна.

4. Изграждане на специфицирана хипотеза.

Често хипотезите, които изглеждат правдоподобни на пръв поглед се оказват неподходящи за решаването на конкретен математически проблем. Когато обобщената хипотеза се развие до своите следствия и решаващият може да оцени специфичната и приложимост тя се преформулира. Първоначално, изградената хипотеза винаги има общ характер, за да бъде тя максимално ефективна е необходимо да бъде уточнена т.е. от обща да се превърне в специфицирана. Процесът може да се изрази с помощта на символи и знаци.

GH ( Kn+1->Kn + m->Kn + m + p) FH

GH– обща хипотеза; Kn– последователни стъпки; m- обекти в проблемната задача; p- връзки и зависимости между обектите; FH- специфицирана хипотеза

Специфицираната хипотеза не е съотнесена с данните и обектите в математическата проблемна ситуация, а с крайната и цел.

5. Създаване на убеждения.

Потвърждаването на хипотезата води до създаване на убеждение за нейната правилност и избор на стратегия, което е следващият етап от процеса на решаване на математически проблеми. Разбира се, окончателното потвърждаване на една хипотеза се извършва, когато ученикът намери решение на проблемната ситуация, но съществуват индикатори( решаване на подцели), които потвърждават нейната правилност.

За да се проследи процеса на хипотезиране нека бъде разгледана следната проблемна задача.

Беден лодкар седял на брега на реката и мислел как да спечели пари. Пред него се появил богат чорбаджия и му предложил да удвоява парите за всяко преминаване през реката, но в замяна лодкарят ще му дава по 24 лева. Голяма била радостта на лодкаря, когато приел условието, но за негова изненада след третото преминаване останал без пари. Колко пари е притежавал лодкарят първоначално?

Първоначално, след прочита на задачата се поражда догадката. Ученикът предполага, че ще трябва да извърши съвкупност от аритметични операции, но не знае как да ги организира в система. Следва идеята, че след като парите ще се увеличават и намаляват аритметичните операции, необходими за разрешаването ще са умножение (удвояват) и изваждане (лодкарят ще му дава по 24 лева). Изгражда се обобщената хипотеза, че правилното организиране на аритметичните действия ще доведе до решението. Позовавайки се на наличната информация и данни ученикът съставя специфицирана хипотеза. Тя организира предоставените данни и отношенията между обектите в следната систематична последователност.

Не е известно началното количество пари, с които е разполагал лодкарят за това то се обозначава с празно квадратче. След като за първото преминаване тези пари ще се удвоят квадратчето се умножава по две, но чорбаджията ще получи 24 лева следователно от произведението е необходимо да се извади 24. В условието е посочено, че след  третото преминаване лодкарят остава без пари. Следователно общият брой преминавания са три, от което следва извода, че първоначалният алгоритъм на действие е необходимо да се повтори още два пъти. Така организирани данни подсказват на ученика, че необходимата стратегия за решаване е „отзад напред”. Когато се извършат първите аритметични операции и те позволят прилагането на следващите се появява и убеждението за правилността на хипотезата.

Хипотезирането е  процес, който може да се определи като изцяло когнитивен, защото е свързан с анализиране на задачата, синтезиране на информацията и правене на обобщения.

Д.В. Вилкеев  посочва два пътя за изграждане на хипотези:

• Индуктивен, по който хипотезата се изгражда на основата на факти и явления, известни от житейския опит на ученика, получени в резултат на наблюдение и експеримент.
• Дедуктивен, който се основава на теории, принципи, закони и правила.

Изграждането на хипотези по дедуктивен начин е процес, който според М.Махмутов може да поеме по два пътя: 1) пътя на пренос на общи принципи и закономерности в конкретната проблемна ситуация и 2) пътя на аналогиите. В първия случай предположението се прави въз основа на съществуващи закономерности, които трябва да се проверят опитно. Така пътя на познанието се осъществява като се въведат нови закони, правила, принципи, основаващи се на вече съществуващи такива. Във втория случай се осъществява тясна връзка между преноса и аналогията. По аналогия се използва такъв сбор от информация, която корелирайки с наличната не се изключват една друга.

Много автори смятат, че индукцията и дедукцията не са отделни пътища за създаване на хипотези, а процеси, взаимно свързани в единната система на хипотезиране. От тук следва заключението, че процесът на изграждане на хипотези преминава през етапи на индуктивни и дедуктивни разсъждения като индукцията, преминаваща от фрагментарни детайли към обща картина на ситуацията способства за създаването на обобщени хипотези, а дедукцията подпомага изграждането на специфицираната хипотеза, тъй като спомага видоизменянето на първоначалното предположение въз основа на интерпретиране на изолирани детайли.

Учебно-възпитателната дейност непрестанно изправя учениците пред огромен диапазон проблеми, които изискват разрешаване. Ето защо не може да се изведе една единствена когнитивна операция, наречена „решаване на проблеми”. Този процес включва различни когнитивни процеси като превесът на някои от тях се определя от отделните случаи. Това обаче не изключва подхождането към проблемите да се прави по определен систематичен начин.

Решаването на проблемни ситуации е процес, при който се търсят решения, като се предлагат хипотези и се провежда изследователска дейност за тяхното доказване. Процесите на хипотезиране са ключови в избора на подходяща стратегия и изграждане на цялостна концепция за решавания проблем. Това са сложни ментални пътища за дедуктико-индуктивно организиране на наличните данни и обекти в нова система, целяща да преодолее наличното противоречие.  Когато противоречието е преодоляно е премахнат и проблемният елемент от проблемната ситуация. Това означава, че процесите на хипотезиране преобразуват математическата проблемна ситуация в обикновена математическа ситуация, а това  от своя страна превръща първоначалното чувство на неудовлетвореност и неспособност в увереност и задоволство от успешното решаване на задачата.

 

Литература / Reference:

1. Дюи Д. Как мислим ИК Минерва 2002
2. Матюшкин А. М. Проблемнье ситуации в мишлении и обучении М., 1972
3. Махмутов М. И. Организация проблемного обучения в школе М., 1977
4. Оконт,В. Проблемното обучение.С.,1986
5. Пойа Д. Как да се решава задача С.,1972
6. Пирьов Г. Психологически проблеми на мисленето С., 1979
7. Стърнбърг Р. Когнитивна психология С., 2012
8. Anderson, B., Pingry, R. E. Problem solving in mathematics Washington 1973
9. Charles, R, Lester, F. Teaching problem solving:What Why and How, Palto Alto 1982