Abstract:The article presents the applications of Papy’s minicomputer for teaching number composition in a fun, different way. It offers a modification of the original version and several exercises to practice learning the numbers up to 100 and operations using them. Didactically, the article provides opportunities to create multiple tasks and games to help develop the mathematical capabilities of young pupils.

За ролята на занимателното в обучението по математика в началните класове е изписано много. Положителните емоции са едно от условията за непреднамереното внимание и запомняне и са в състояние да влияят на процесите на възприятието и мисленето. Оказват влияние и върху развитието на потребностно-мотивационната и познавателната страни на личността. Затова съществен елемент на урока по математика е създаването  на благоприятна емоционална обстановка в класа, а един от начините е включването на занимателното чрез различни средства: дидактични игри, задачи, гатанки, ребуси и др. Занимателното в урока по математика не бива да се отъждествява единствено с развлекателното. Изборът на дадено средство трябва да се определя от възможностите на това средство да развива общите математически способности, да осигурява баланса между емоционалното и рационалното в занимателната дейност.

Едно такова средство е „Малкият компютър“ на Папи – дидактичен материал, който предоставя големи възможности за разработване на многобройни упражнения и варианти на игри, приложими в различни видове уроци и в различни моменти от урока по математика, в задължителните и избираемите часове. Може да се използва и у дома – индивидуално от ученика или като семейна игра със състезателен характер. Въпреки че „Малкият компютър“ е известен отдавна и в България, сякаш остава непознат в класната стая. Целта на тази разработка е да запозная по-широка аудитория с възможностите му, като споделя и опит от практиката си като начален учител.

Жорж Папи (1920-2011)  и Фредерик Папи-Ленгер(1921-2005) – семейство белгийски математици и педагози, през 60-те години на ХХ в. чрез своя „Малък компютър” предлагат интересен и забавен начин за изучаване на състава на числата. Идеята е заимствана от „цветните числа“ на Жорж Кюизинер и измислят квадрат (16 х 16 см), разделен на четири по-малки квадрата (8 х 8 см), оцветени в четири цвята, като всеки цвят има зададена стойност. За демонстративна работа на учителя се използва магнитна дъска с размери 40 х 40 см. Жетон, поставен в дадено поле, приема стойността на полето. В един такъв квадрат се представят едноцифрените числа, с поставянето на допълнителен квадрат вляво се представят двуцифрени числа, като единият е за единиците, а другият – за десетиците. С добавяне на квадрат за стотиците се представят трицифрени числа и т.н. (Vaneva, 2009). По този начин „малкият компютър“ открива възможности за използването му във всички класове на началната училищна степен. Изискване за моделиране на числото е то да бъде представено с възможно най-малко жетони. Предлага се и начин за прехвърлянето на единици в реда на десетиците, на десетици в реда на стотиците и т.н. – като се преобразува даденото число, така че в лявата колона (кафяво и червено поле) да се получава 10, 100, 1000 и т.н. (Papy, 1970).

Фиг. 1. Подредба на квадратите и стойности на различните цветни полета.

9=8+1

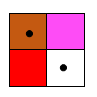
Фиг. 2.Едноцифрени числа

 

38= 20+10+8

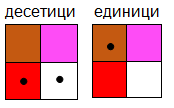
Фиг. 3. Двуцифрени числа

 

693= 400+200+80+10+2+1

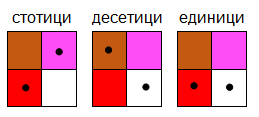
Фиг. 4. Трицифрени числа

 

4075 =4000+40+20+10+4+1

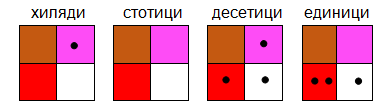
Фиг. 5. Многоцифрени числа

 

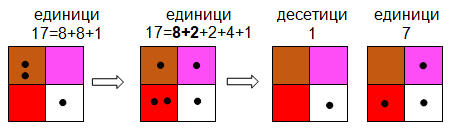
Фиг. 6. Преобразуване на единици в десетици и прехвърлянето им в квадрата на десетиците

 

„Малкият компютър“ на Папи бързо добива известност и почти веднага започват да се разработват различни игри на основата на стандартната версия, като в предложената в края литература могат да се видят такива (Minicomputer Games, 1979). AdelynC. Muller съчетава цветните пръчици на Ж. Кюизинер и „компютъра“ на Папи, като предлага задачи от събиране и изваждане, подходящи за началните класове (Muller, 1971). В българската методическа литература има разработки за приложението на „малкия компютър“ и пръчиците на Кюизинер в детската градина – на А. Велева, В. Ванева. В „Методика на обучението по математика в началните класове“ В. Ванева разглежда теориите на обучението и конкретната работа на редица теоретици и практици, сред които Кюизинер и Папи, оказали влияние върху съвременните програми за обучение по математика и начините за работа.  Представя в общ вид поотделно и двата дидактични материала и затова считам за полезно да се представи една от възможностите за съчетаването им и в обучението по математика в началните класове.

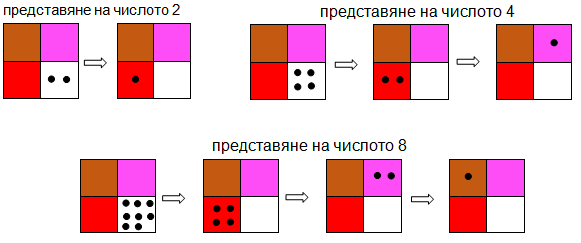
Вместо разноцветния квадрат се използва едноцветен, а жетоните се заменят с пръчици със сечение 1 кв.см в различни цветове (по Кюизинер): бели – числото 1 (1 см), червени – числото 2 (2 см), розови – число 4 (4 см), кафяви – число 8 (8 см).

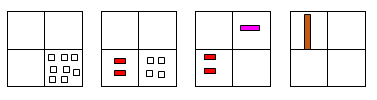
. Фиг. 7. Варианти на числото 8 по AdelynMuller

 

При събирането на едноцифрени числа с преминаване на десетицата сборът се „записва“ в квадрата на единиците. След това полученото число се преобразува, така че вляво да се получи 10, като тази десетица след това се прехвърля в квадрата, изобразяващ десетиците.

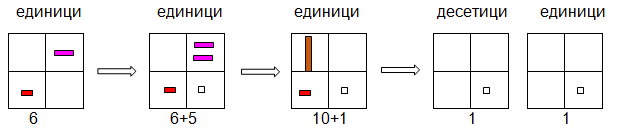
Фиг. 8. Събиране на едноцифрени числа с преминаване на десетицата (Muller, 1971)

 

Събиране на двуцифрени числа с двуцифрени с преминаване се извършва, като се съберат десетици с десетици, и се записват в квадрата на десетиците. Единиците се събират и се записват в квадрата на единиците. Числото в квадрата на единиците е по-голямо от 10, то се преобразува, така че в лявата част да се получи десетица от 8 + 2, която да се прехвърли в квадрата на десетиците.

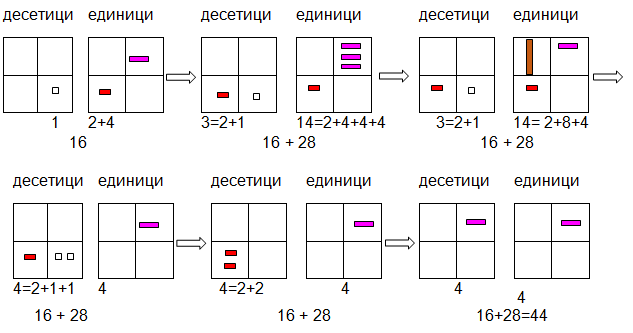
Фиг. 9. Събиране на двуцифрени числа с преминаване

При изваждането малките квадрати се разделят с пунктир. Ако вземем за пример израза 9 – 4, първо се записва умаляемото 9 отляво на пунктира, след това отдясно – умалителят 5. Ако 9 е записано като 8 + 1, а 5 като 4 +1, то трябва да се замени 8 с 4 + 4. Накрая се изпълнява 4 – 4 и 1 – 1 и се получава разликата.

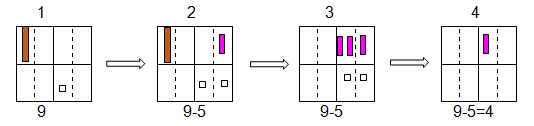
Фиг. 10. Изваждане на едноцифрени числа (Muller, 1971)

Този начин на „записване“ на умаляемо и умалител се прилага и при изваждане на по-големи числа.

Вариант на използване на „Малкия компютър“ в първи и втори клас

По-долу предлагам вариант на използване на „Малкия компютър“ като дидактичен материал при изучаването на числата до 100, заемайки идеята на Папи за цветовите стойности, но използвайки само един квадрат. По наблюдения от учителската ми практика съдя, че за по-голямата част от първокласниците „миникомпютърът“ е непознат, затова ще акцентирам върху основни моменти от представянето му и запознаването с правилата за работа с него.

Целите на упражненията се отнасят до: разширяване на възможностите за по-различно и интересно изучаване на математическите понятия; усвояване на знания за състава на числата; добиване на представа, че числата могат да се представят по различни начини; достигане до заключението, че за една задача могат да се открият много решения; развитие на уменията за бързо устно смятане; развитие на уменията за откриване на зависимости; развитие на умения за моделиране.

Необходими материали: по един квадрат за всеки ученик и демонстративен такъв за учителя. В жетони могат да се превърнат изрязани кръгчета от картон, бобени зърна, малки копчета (желателно е да са еднакви) и др. – нужни са около 20-40 бр.

Важна част от работата с „Малкия компютър“ е запознаването на първокласниците с основните правила и принципни положения на действие. За начало учениците трябва да усвоят стойността на всеки цвят от малките квадрати и да осъзнаят, че един жетон в дадено поле означава съответната стойност – един жетон в бяло поле е числото 1, един в червено поле е 2 и т.н. На видно място в класната стая трябва да се постави квадрат с изписаните стойности в полетата.

Примерни упражнения: сложи един жетон на бяло поле. Кое е числото?; Премести жетона в червено поле. Кое число получи?  т. н.

В следващия етап е целесъобразно да се изпълняват упражнения, свързани с разбиране и усвояване на принципа на замяна на жетоните – 2 жетона от малкото поле се заменят от 1 от следващото по големина поле. За целта препоръчително е да се започне от бялото поле и последователно да се премине до кафявото:

2Б ➞ 1Ч; 4Б ➞ 2Ч ➞ 1Р; 8Б ➞ 4Ч ➞ 2Р ➞ 1К

Примерни упражнения: постави един жетон в бяло поле. Кое число е това? За числото 2 колко жетона трябват в бяло поле? Колко жетона ти трябват за числото 2 в червено поле? Двата жетона от бялото поле с колко жетона от червено поле ще замениш? т. н.

Фиг. 11. Замяна на жетоните

След усвояването на основните правила се задават задачи за състава на числата до 10. Възможността да бъдат изпълнени многобройни варианти на упражнения улеснява разбирането у малките ученици, че всяко число може да бъде получено от две или повече други по-малки числа. Примерни задачи:

• Поставете 3 жетона в бяло поле. Кое число е това?
• Наредете числото 3 в различни полета.
• Представете числото 4 в едно поле.
• Представете числото 5 в бяло и розово.
• Представете числото 6 с възможно най-малко жетони.
• Представете числото 8 в две полета.
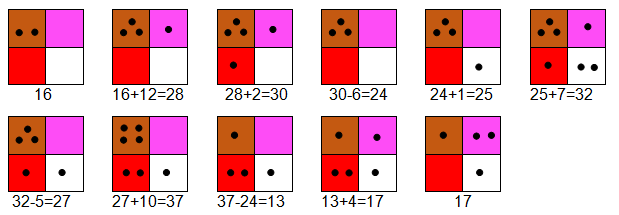
• Представете числото 9 по всички възможни начини(фиг. 12).
• Ако поставим един жетон в кафяво и един в червено поле, кое число е това?
• Поставете 3 жетона в бяло поле. Добавете 2 в червено поле. Кое число се получи? Как можем да запишем с израз? (1+1+1+2+2=7; 3+4=7)
• Поставете 5 жетона в червено поле. Кое число е това? Махнете 2 жетона. Кое число остана? Как ще се запише с израз? (2+2+2+2+2=10 10-2-2=6 или 10-4=6)
• Поставете 2 жетона в бяло поле, 2 жетона в червено и 1 жетон в розово поле. Кое число е това? Колко жетона и от кое поле ще махнете, за остане 6? Как ще се запише с израз? 

 

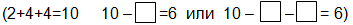
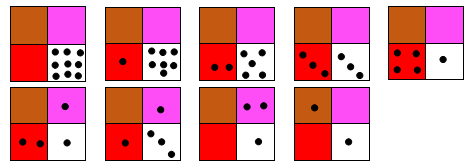
Фиг. 12.Всички варианти на представяне на числото 9

Ясно е, че колкото по-големи стават числата, толкова повече са и вариантите, по които могат да се „запишат“. Затова учителят трябва да предвиди достатъчно време, да помисли и за формата, в която ще организира реализацията, както и начин за проследяване на резултатите (по-долу предлагам такъв).

При изучаването на числата от 11 до 20 във варианта на „малкия компютър“, който предлагам, упражненията се изпълняват само с един квадрат – този на единиците. Освен предложените вече упражнения при изучаването на числата до 10 може да се включат и такива, при които учениците да представят числата като получени от десетици и единици. Например: Колко десетици и колко единици има числото 15? Запиши десетицата с възможно най-малко жетони. Запиши единиците в други полета(фиг.13).

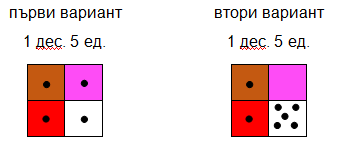
Фиг. 13.Представяне на 15 с изискване за групиране на десетицата и единиците

Примерна задача в няколко хода при изучаване на числата от 11 до 20 (фиг. 14):

• Наредете числото 12 в кафяво, червено и бяло поле.
• Към 12 (в кафяво, червено и бяло поле) добавете 1 жетон в розово поле. Кое число получихте?
• Направете така, че от числото 16 (в кафяво, червено, бяло и розово поле) да остане 10.
• Как ще запишем с „верижка? (фиг. 15)

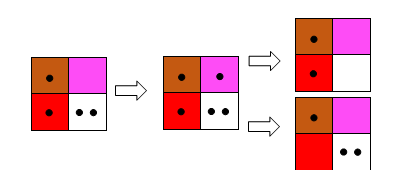
Фиг.14. Последователност на действията от примерната задача

 

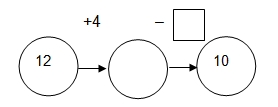
Фиг.15Съставяне на модел на верижка по действията от примерната задача

 

В първи клас при изучаване на числата 10, 20, 30…100 с използването само на един квадрат е целесъобразно първо да се моделира една десетица и след това същата конфигурация да се изобрази толкова пъти, колкото е изискваният в задачата брой десетици.

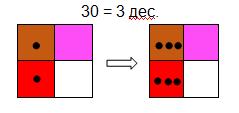
Фиг. 16Представяне на кръгли десетици

 

Използването на един квадрат-„компютър“ може да продължи и във втори клас при изучаването на числата до 100 и действията с тях. Моделирането на числа в едно поле е отлична подготовка за действие умножение като сбор на равни събираеми и начин за  запаметяване на таблиците с числата от „компютъра“. С различни упражнения може да се онагледи делението и да се извършват пресмятания.

Примерна задача: представи числото 24 в едно поле. Как можеш да запишеш със събиране? Запиши с умножение. Раздели жетоните в три еднакви групи. Кое число показва всяка група? (фиг. 17)

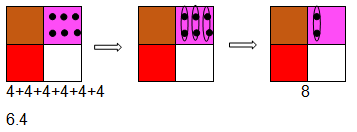
Фиг. 17

Във втори клас моделирането на числа на„малкия компютър“ в различни полета открива възможности за учителя за задаване на упражнения, свързани със записване на съставни числови изрази по зададения модел и извършване на пресмятания, като се прилагат знанията за реда на действията (фиг. 18)

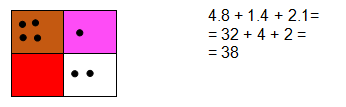
Фиг.18

 

Упражненията с „малкия компютър“ нямат ограничения за формата на организация на класа. Подходящи са за фронтална, индивидуална и групова работа (2-4 ученици за работа с един „компютър“). Предложените по-долу игри са за работа в екип.

 

Игра „Кой първи ще открие числото“

Образователно съдържание: развитие на уменията за събиране и изваждане на числата до 100.

Необходими материали: един „компютър“, 10 жетона, лист за записване на действията.

Правила: учениците са разпределени в екипи по двама (съседи по чин). Всички екипи получават една и съща задача, която трябва да пресметнат с „малкия компютър“. Поставя се условието всяко прибавено и извадено число, както и отговорът да бъдат „записвани“ с възможно най-малко жетони. На листа, който предварително е разграфен, се отбелязват последователните действия и числата. Учениците сами си разпределят отговорностите в екипа – единият смята, другият записва резултата. Победител е екипът, който първи стигне до верния отговор и е отразил правилно всичките си действия.

Задача: В началото се обяснява, че всяка стрелка нагоре означава събиране, а стрелка надолу – изваждане:

Фиг. 19.Решение на задачата в „Кой първи ще открие числото“

 

Лист за записване на действията и числата:

1	16	2К
2	+12	1К, 1Р
3	+ 2	1Ч
4	– 6	1Р, 1Ч
5	+ 1	1Б
6	+ 7	1Р, 1Ч, 1Б
7	– 5	1Р, 1Б
8	+ 10	1К, 1Ч
9	– 24	3К
10	+ 4	1Р
11	17	1К, 2Р, 1Б

 

Игра „Кой ще събере най-малко жетони“

Образователно съдържание: представяне на състава на числата до 100.

Необходими материали: един квадрат-„компютър“, жетони, лист за записване на числата.

Правила: учениците са разпределени в екипи по двама. Всички екипи получават една и съща задача – учителят съобщава последователно числата или ги предоставя в началото на всеки екип. Условието за представяне на всяко число с възможно най-малко жетони се съдържа в наименованието на играта и екипите трябва да проявят съобразителност. Жетоните за всяко число след моделирането му на „компютъра“ се отделят настрана, за да бъдат преброени накрая всичките. Учениците сами си разпределят отговорностите в екипа – единият записва всяко число на „компютъра“, другият го записва на листа (например, 24 – 3К). Победител е екипът, който е събрал най-малко жетони.

Ако оригиналният картонен квадрат-„компютър“ се счита за твърде остарял, съвременните условия предоставят възможност на учителите да използват за демонстративни упражнения вместо магнитна дъска мултимедията, а учениците да изпълняват упражненията и игрите на компютър – достатъчен е един слайд, изработен с Microsoft Power Point при липса на по-усъвършенстван модел. При всички случаи заниманията с „миникомпютъра“ ще допринесат за математическото развитие на децата.

ЛИТЕРАТУРА

1. Ванева, Виолета.(2009). Съвременни математически програми – предимства и недостатъци, В: Методика на обучението по математика в началните класове.Теория, тестове, план-конспекти. Русе, УИ „Ангел Кънчев“
2. MinicomputerGames.(1979). Comprehensive School Mathematics Program (CSMP). CEMREL Inc, St. Louis, Mo., USA.http://stern.buffalostate.edu/(последен достъп 29.05.2020 г.)
3. Muller, A. (1971).An Adaptation of Papy’s Minicomputer. Cuisenaire Company of America, Inc. 12 Church Street, New Rochelle, NY. 10805. http://stern.buffalostate.edu/(последен достъп 29.05.2020 г.)
4. Papy, Frederique.(1970).Papy’s Minicomputer.Mathematics Teaching, The Bulletin of the Association of Teachers of Mathematics, No. 50. http://www.rkennes.be/(последен достъп 29.05.2020г.)

REFERENCES

1. Vaneva, Violeta. (2009). Savremenni matematicheski programi – predimstva i nedostatatsi, In: Metodika na obuchenieto po matematika v nachalnite klasove. Teoria, testove, plan-konspekti. Ruse, UI “Angel Kanchev”
2. Minicomputer Games. (1979). Comprehensive School Mathematics Program (CSMP). CEMREL Inc, St. Louis, Mo., USA.http://stern.buffalostate.edu/(posleden dostap05.2020 г.)
3. Muller, A. (1971). An Adaptation of Papy’s Minicomputer. Cuisenaire Company of America, Inc. 12 Church Street, New Rochelle, NY. 10805. http://stern.buffalostate.edu/(posleden dostap 29.05.2020 г.)
4. Papy, Frederique.(1970).Papy’s Minicomputer. Mathematics Teaching, The Bulletin of the Association of Teachers of Mathematics, No. 50. http://www.rkennes.be/(posleden dostap05.2020г.)