Abstract:From a pedagogical point of view, the development of children’s skills in using the modeling method is important for two reasons: first, the modeling activity contributes to the development of cognitive function; secondly, mathematical concepts are abstract and can only be learned by children with the help of models. Modeling is widely used in learning mathematics material in kindergarten. At the same time, in preschool education in Bulgaria, the modeling method is applied as a means of mathematical learning (children work with ready-made models), but not for developing the skills for modeling mathematical relations. In this respect, the aim of the present paper is to reveal opportunities for developing the modeling activity of preschool children as a prerequisite for their intellectual and, in particular, mathematical development.

Моделирането е метод на познание, който се основава на символната функция. В основата му стои заместването на реални обекти с други обекти (практическо моделиране) или с графически изображения (графическо моделиране). В. Василева посочва, че моделирането представлява процес на създаване, изследване и използване на модели (V. Vasileva, 2016). Моделът фиксира в достъпна нагледна форма изучаваните свойства и отношения между обектите. По този начин се добива познание за обекта-оригинал.

В педагогически аспект развитието на уменията на децата да използват метода моделиране е от важно значение поради две причини. Първата е аргументирана от Н. Забродина и М. Стожарова по следния начин – моделиращата дейност съдейства за развитие на познавателната функция: получаване на нови знания и стимулиране на нагледно-схематичното мислене като преходен етап от нагледно-образното към словесно-логическото. (N. Zabrodina, M. Stozharova, 2014)

На второ място необходимостта децата да овладеят моделирането като метод на познание се обосновава от Д. Гълъбова и Н. Делчева, които посочват, че математическите понятия са абстрактни и могат да се изучават от децата само с помощта на модели (D. Galabova, N. Delcheva, 2016).

Моделите, които се използват при формиране на елементарни математически представи могат да бъдат материални (например модели на геометрични фигури, жетони и пръчици за представяне на числа) и идеални (образи, знаци, схеми, планове). Моделирането се използва широко при усвояването на материала от петте ядра на образователно направление „математика“: децата моделират числата с жетони; изучават техния състав от по-малки числа чрез разноцветни кубчета; представят отношенията между множествата с диаграми Вен-Ойлер; решават текстови задачи с помощта на схеми; съставят и използват план на занималнята; обозначават сезоните, дните на седмицата, месеците с геометрични фигури или цветни картончета и т.н. В същото време е вярна констатацията на Д. Гълъбова и Н. Делчева, че в предучилищното образование в България методът моделиране се прилага като средство за математическо обучение (децата работят с готови модели), но не и за развиване уменията за моделиране на математически отношения (D. Galabova, N. Delcheva, 2016). Във връзка с това целта на настоящата разработка е да се разкрият възможности за развиване на моделиращата дейност на децата в предучилищна възраст като предпоставка за тяхното интелектуално и в частност математическо развитие. Това е в съответствие с посочената от Г. Георгиева цел на обучението по математика в детската градина, то да осигурява не само знания, но и да е насочено към развитие на общата познавателна дейност на децата (G. Georgieva, 2021).

Предложените по-долу активности съответстват на трите етапа при запознаване с метода моделиране, посочени от В. Ванева: първи етап – практическо моделиране; втори етап – изработване на графична схема от децата; трети етап – работа с готови графични схеми (V. Vaneva, 2006).

Децата се въвеждат в моделирането, като решават все по-усложняващи се задачи в дадената по-долу последователност.

• Практическо моделиране

При този вид моделиране изучаваните обекти се заместват от други предмети (жетони, кубчета, пръчици и др.). Основната познавателна задача на първоначалния етап на работа е формулирана от Е. Михайлова, А. Носова и др. по следния начин: развитие на умението да се установи отношението „обознначавано – обозначаващо“ и да се обогати опита по заместване на обекти (E. Mihaylova et al, 2008). Подходящо е за целта да се изходи от игрова ситуация, тъй като децата имат опит за игрово заместване на едни предмети с други.

Може да се организира ситуация на тема „На пазар“, в която учителят е в ролята на добродушна бабичка, продаваща на пазара свежи плодове и зеленчуци от своята градина. На щанда се подреждат кутии („щайги“); във всяка от тях има детайли от пластмасов конструктор в определен вид и цвят (например паралелепипеди, сфери, триъгълни призми, цилиндри в зелен, жълт, червен, лилав, оранжев цвят и различни големини). До пазара има банка – масичка с табелка и дете – „банкер“, който има сейф, пълен с пари (жетони). Децата седят около масичките, на всяко от които има по едно празно портмоне, кошничка и играчки от готварски комплект – тенджера, дъска и нож за рязане, лъжица. Учителят предлага на всяко „семейство“ (групите по масички) да си изтеглят пари от банката и да си купят пресни плодове и зеленчуци. По едно дете от всяко семейство тегли пари от банката и след това пазарува от бабата, като посочва кутия с детайли и назовава желания продукт (домати или ябълки – червени сфери; краставици – зелени цилиндри, моркови – оранжеви призми и т.н.). След като децата напазаруват се прибират у дома и сготвят със закупените продукти. Накрая на ситуацията бабата отива на гости при всички, пита какво има в тенджерите, опитва и хвали децата.

През следващите дни в ситуация по математика се припомня играта и се предлага на децата отново да заменят едни предмети с други, но този път за да си помогнат да решават задачи. Заместването не трябва да е самоцелно – използва се, когато обектите на познание не могат да се изучат непосредствено. Например при необходимост от сравняване на множества, които не могат да се съпоставят непосредствено.

На магнитната дъска се поставя илюстрация на простир, на който има различни дрехи, сред тях 6 ръкавички. Под картината се подреждат фигури на три деца. Съобщава се задачата – да се определи има ли за всяко дете чифт ръкавици. Предлага се върху всяка ръкавица на картината да се постави жетон – жетоните ще заместят ръкавичките. След това се поканват деца от групата да поставят по два жетона под фигурите на дъската и така да установят дали за всяко дете има по две ръкавички.

Практическо моделиране може да се използва и за „съхраняване“ на числови данни, които не могат да се запомнят непосредствено.

Учителят разказва история, като преди това предупреждава децата, че от тях се иска накрая да сравнят по брой нещата, за които се говори. Могат да си помогнат, като използват жетони/бобчета/други дребни предмети. Всяко дете поучава изрязани от хартия обектите, за които се говори в историята и докато слуша историята, поставя под тях толкова бобчета, колкото казва учителят: „Малката русалка видяла на морското дъно 3 миди, 4 рака, 2 морски звезди, 5 водорасли, 1 риба“. След това учителят задава въпроси, а децата вдигат съответното изображение: „Кои са били най-многобройни на морското дъно?“ (водорасли). „Кои са били най-малко?“ (риба) „Кои са били с едно повече от морските звезди?“ (миди). Децата, които се забавят или вдигнат грешно изображение, изгарят.

При поставянето на задачите е важно моделирането да не е самоцелно, а да подпомага дейността на децата, за да осмислят практическата значимост на метода.

• Изработване на графична схема

Графическите схеми подпомагат онагледяването на вътрешни съществени взаимовръзки. По този начин те улесняват осмислянето на условието на дадена задача и намирането на път за нейното решаване. За да осъзнаят децата значението на графите е добре да им се даде възможност самите те да изработят такива изображения. Чрез близки до 5-7-годишните житейски ситуации се обяснява, че точките заместват реални обекти; всяка група предмети, които сме отбелязали с точки, оглаждаме с кръг или овал.

Много добър пример за това дава Д. Гълъбова. На магнитната дъска е поставен бял лист и е скициран Ежко. Учителят разказва: „Есен е. Ежко седи под една ябълка и си мисли за зимнината. И ето, хоп – една ябълка паднала върху него (учителят рисува една червена точка), и още една, и още една и т.н. Да оградим всичките ябълки, които Ежко ще отнесе вкъщи. Колко ли са те? Как да разберем? (ще преброим точките) само ние знаем, че тази картинка са ябълките на Ежко. Такива картинки се наричат „скрити картинки“ на броя на предметите. Нарисувайте с точки членовете на вашето семейство, а аз ще позная колко сте вкъщи.“ (Д. Гълъбова, 2003, с. 166)

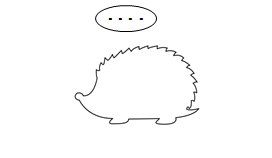
След това, казва Д. Гълъбова, учителят трябва мотивирано да запознае децата със стрелката като знак за отношение между елементите в множествата. Поради това, че стрелката изразява отношението (връзката) и носи словесна информация, пред децата се казва, че „стрелката говори“. Те и сами могат да стигнат до този извод, ако ги поставим в ситуация за разчитане на пътни знаци. Житейският им опит позволява да разчетат знаците „разрешено само напред“, „завий наляво“. Сами стигат до извода, че стрелката казва какво да се прави. Запознават се с цветни стрелки, които говорят и свързват обекти от едно или две множества. (Д. Гълъбова, 2003, с. 165-166)

Децата трябва да стигнат до разбирането, че създаването на модели може да ни помогне много при решаването на задачи. Подходящи за предучилищната възраст са представени по-долу.

Сърдитко е по-голям от Глупи, но е по-малък от Сънливко. Кой е на-голям от тримата. Хайде да разберем, като си помогнем със стрелки. Стрелката казва „Аз съм по-голям от теб“. Стрелката сочи към по-малкия. Затова стрелката между Сърдитко и Глупи ще сочи към Глупи – той е по-малък. Как да поставим стрелката между Сърдитко и Сънливко, като знаем, че Сърдитко е по-малък? Кой от тримата е най-голям?

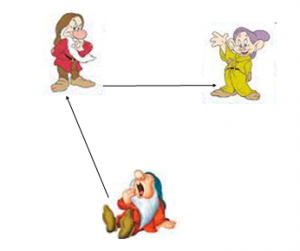
Конят тича по-бързо от заека и по-бавно от гепарда. Кое животно тича най-бързо?

Русокоска и Чернокоска  имат домашни любимци. Едната коте, а другата – куче. Какво животно има Русокоска, ако Чернокоска няма котка?

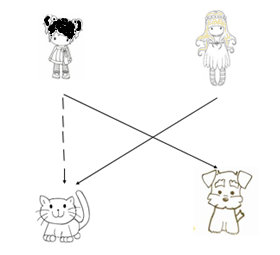
• Работа с готова графична схема

След като децата стигнат до разбирането, че графичните модели се използват за решаването на задачи, може да им се предложат готови графи, с които да оперират.

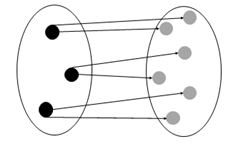
Черните точки представляват кученца, а сивите – кокали. Свържете черните и сивите точки със стрелки, за да проверите има ли за всяко куче кокал.

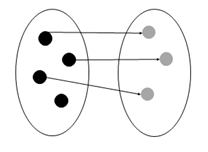
Черните точки са деца, а сивите – техните ръкавички. Свържете черните със сивите точки така, че да разберем дали за всяко дете има чифт ръкавици.

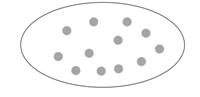
Сивите точки са цветята, поникнали на полянката. Деца искат да наберат букети за майките си. Във всеки букет трябва да има по три цветя. Оградете, за да проверите за колко майки ще има букети.

Приложението на предложените активности ще даде възможност на децата осъзнато да използват метода моделиране. Това е предпоставка те да извлекат от него максимална полза по отношение на общоинтелектуалното и математическото си развитие при овладяването на конкретно образователно съдържание. Задачата за целенасоченото развитие у подрастващите на моделиращата дейност е в съответствие със съвременните обществени потребности образователната система не само да обезпечава овладяването на определен обем от знания, но и да развива мисловните умения.

ЛИТЕРАТУРА

1. Ванева, В. (2006). Педагогика на овладяване на елементарни математични представи. Русе: Печатна база при Русенския университет „Ангел Кънчев“.
2. Василева, В. (2016). Дидактическото моделиране в обучението – основа за личностно развитие на учениците. Педагогически новости, Vol 1, 78 – 82.
3. Георгиева, Г. (2021). Методически насоки за приложение на Bee-Bot програмируема играчка в обучението по математика в детската градина. Педагогически новости, Vol 1, 16-24.
4. Гълъбова, Д., Н. Делчева. (2016). Дидактичен модел „Конструктивна математика за деца“. Педагогика, 88 (9), 1159 – 1170.
5. Забродина, Н., М. Стожарова. (2014). Развитие основ логического мышления дошкольников с помощю метода моделирования (на материале математики). Science prospects, Vol. 12 (63), 16 – 20.
6. Михайлова, Е., А. Носова и др. (2008). Теории и технологии математического развития детей дошкольного возраста. – Санкт-Петербург: Детство-пресс.

REFERENCES

1. Vaneva, V. (2006). Pedagogika na ovladyavane na elementarni matematichni predstavi. Ruse: Pechatna baza pri Rusenskia universitet „Angel Kanchev“.
2. Vasileva, V. (2016). Didakticheskoto modelirane v obuchenieto – osnova za lichnostno razvitie na uchenitsite. Pedagogicheski novosti, Vol 1, 78 – 82.
3. Georgieva, G. (2021). Metodicheski nasoki za prilozhenie na Bee-Bot programiruema igrachka v obuchenieto po matematika v detskata gradina. Pedagogicheski novosti, Vol 1, 16-24.
4. Galabova, D., N. Delcheva. (2016). Didaktichen model „Konstruktivna matematika za detsa“. Pedagogika, Vol. 88 (9), 1159 – 1170.
5. N.. M. Stozharova. (2014). Razvitie osnov logicheskogo myshleniya doshkolnikov s pomoshchyu metoda modelirovaniya (na materiale matematiki). Science prospects. Vol. 12 (63). 16 – 20.
6. E.. A. Nosova i dr. (2008). Teorii i tekhnologii matematicheskogo razvitiya detey doshkolnogo vozrasta. – Sankt-Peterburg: Detstvo-press.