Развитие на алгоритмичните умения в предучилищна възраст
доц. д-р Ася Велева
Русенски университет „Ангел Кънчев“
aveleva[at]uni-ruse.bg
Development of algorithmic skills in preschool age
Assoc. Prof. Asya Veleva, PhD
University of Ruse „Angel Kanchev”
aveleva[at]uni-ruse.bg
Abstract:Algorithmic skills are very important for successful implementation in contemporary high-tech world. Algorithms are used in mathematics and in computer science as well in everyday activities. Tasks with algorithms contribute to the development of logical thinking, planning skills, selfcontrol, skills for transfer of a method of solving one task to another. Therefore many authors recommend the development of algorithmic skills in preschool children. However they don’t offer methodological recommendations for the teacher how to teach children to use block diagrams. The description of algorithms in block diagrams corresponds very well to the peculiarities of visual thinking in this age. In this context the main purpose of current paper is to present methodological sequence of tasks and exercises for performing and compiling algorithms in block diagrams for 5-7-year old children. In this way the foundations of digital competence are laid, which is important for life and successful realization in the information society.
ВЪВЕДЕНИЕ
Алгоритмичните умения са важни за успешната реализация в съвременния високотехнологичен свят. Алгоритми се използват в математиката и информатиката, а също и в ежедневните човешки дейности. Задачите с алгоритми съдействат за развитие на логическото мислене, уменията за последователност в планирането и осъществяването на своите действия, за самоконтрол, за точно изразяване на мислите, за пренос на метод на решение на дадена задача върху друга, сходна на нея. Във връзка с това през последните години в научната литература се представят насоки развитие на алгоритмичното мислене на малките ученици. Методически системи в това отношение са разработили например М. Касева, 2015 и Д. Димитров, М. Касева, 2015. Практиката показва, че още в предучилищна възраст е полезно и интересно за децата да се запознаят с различни видове алгоритми. Идеи за това предлагат Д. Гълъбова, 2009, Е. Утюмова, 2016, С. Пархоменко 2020 и др. Цитираните автори представят интересни и развиващи задачи, без да си поставят за цел систематизирането на методически насоки за обучението на децата да използват блок-схеми. Този начин на описание на алгоритмите е особено подходящ за предучилищния период, тъй като съответства на особеностите на мисленето на дадения възрастов етап. От друга страна използването на блок-схеми с деца до 7-годишна възраст е свързано с известни трудности, тъй като те не могат да четат и пишат – командите и условията трябва да се представят само с пиктограми. Във връзка с това целта на настоящия материал е да предложи методическа последователност за обучение 5-7-годишнште деца в използването на блок-схеми при изпълнение и съставяне на алгоритми, базирана на постепенно усложняващи се задачи.
ИЗЛОЖЕНИЕ
Алгоритъмът е набор от точни правила, описващи последователността за извършване на дадени действия, които водят до решаването на определена задача (за постигането на конкретен резултат). Във всекидневието си хората непрекъснато използват алгоритми, т.е. действия изпълнявани в определен ред. Например пресичане на улица, затопляне на храна в микровълнова фурна и мн. др.
Понятието алгоритъм не бива да се бърка с алгоритмичната последователност. Както посочва З. Семадени, най-съществена черта на алгоритмите, е фактът, че при тях всички стъпки трябва да бъдат извършвани механически, без проявяването на каквато и да било самоинициатива от страна на изпълнителя. Благодарение на това определени алгоритми могат да бъдат извършвани от машини. При алгоримичните последователности действията не е задължително да се осъществяват в строго определен ред (З. Семадени, 1976, с. 17). Така например при сервирането на маса може първо да се поставят салфетките, а след това чиниите, но може и обратното. За да се доведат децата до разбирането, че при изпълнението на алгоритъма не бива да се променя редът на стъпките, е целесъобразно да се акцентира върху приложението на алгоритми при работата на машини. Ето защо задачите по-долу са мотивирани сюжетно с програмирането на робот. Той се представя на децата във вид на играчка или илюстрация. Предлага им се да ми дадат име и да го научат да извършва различни дейности, за да е в услуга на хората, като създадат за него компютърни програми, изградени от алгоритми. Обяснява се на децата, че роботът или компютърът са „умни“, благодарение на програмите, които ги управляват. А тези програми се пишат от хората. Фокусът върху стриктното спазване на дадената последователност се постига и чрез използването на блок-схеми при изпълнението и създаването на алгоритми. Дава се възможност и на децата да влязат в ролята на робота, като изпълнят дадени от учителя или съставени от тях алгоритми – казва им се да стартират програмата и да проверят резултата. При това в някои от алгоритмите педагогът може преднамерено да заложи неправилна последователност на действията. Извършвайки ги на практика (или описвайки с думи алгоритъма) децата сами ще установят, че нарушаването на определения ред води до невъзможност за решаване на задачата.
В предучилищна възраст децата могат да се запознаят със следните видове алгоритми:
Линейни алгоритми. При тях командите се изпълняват една след друга в последователността, в която са записани. Действията в линейните алгоритми се изпълняват еднократно. Тези алгоритми могат да се представят в блок-схема от вида на фигура 1, където черната точка означава начало, белият кръг с черна точка – край; в овалите са действията, а последователността им е показана със стрелки.
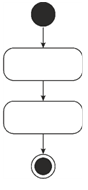
Фигура 1. Блок-схема на линеен алгоритъм
Циклични алгоритми. При тези алгоритми определени действия трябва да се повтарят определен брой пъти или докато не се изпълни дадено условие. Цикличните алгоритми могат да се представят в блок-схема от вида на фигура 2, където условието е дадено в ромб. Словесно се описват така: „Ако (условие) повтаряй командите…“
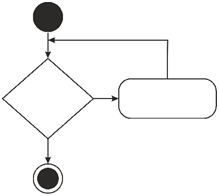
Фигура 2. Блок-схема на цикличен алгоритъм
Разклонени алгоритми. При тях в зависимост от условието се изпълнява една или друга последователност от действия. Тези алгоритми могат да се представят в блок-схема от вида на фигура 3. Словесно разклонените алгоритми се описват така: „Ако (условие), то (една последователност от команди); ако не (условие), то (друга последователност от команди)“.
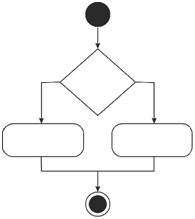
Фигура 3. Блок-схема на разклонен алгоритъм
По-долу е представена методическа последователност от задачи за развитие на алгоритмичното мислене на 5-7-годишните деца чрез използване на блок-схеми.
- Подреждане на последователност от събития в позната приказка в блок-схема на линеен алгоритъм
За децата не е лесно да опишат действията си в последователни еднозначно определени стъпки. Ето защо е подходящо да им се даде възможност първоначално да „видят“ алгоритъма в добре познати приказки, където събитията протичат в точно определен ред. Представя се роботът и се разказва, че той току-що е излязъл от фабриката и все още не може да прави нищо. Предлага се първо децата да го програмират да разказва приказки. Роботът разбира командите, ако са описани в блок-схема. Той знае, че на схемата първо се поставя черна точка, означаваща начало на действията, после всяко действие се посочва в отделен овал и достигането до черната точка в бял кръг означава край. Между действията се поставят стрелки, които показват кое след кое следва. Обясненията се илюстрират в блок-схема и се предлага на децата да разкажат приказката по нея. Фокусира се вниманието върху факта, че ако се променят местата на картинките, роботът грешно ще научи и разказва приказката.

Фигура 4. Линеен алгоритъм „Дядо и ряпа“.
След това се дават празна блок-схема и илюстрации от друга приказка. Едно от децата поставя картините на схемата, а друго – от името на робота разказва приказката.
- Подреждане на последователност от действия за осъществяване на позната дейност в блок-схема на линеен алгоритъм
Предлага се на групата да научи робота да помага в домакинството. На децата се дава празна блок-схема на линеен алгоритъм и серии от картинки, които трябва да се поставят на нея. Например: „Да програмираме робота да полива цветя“ (робот взема празна лейка/ пълни лейката с вода от чешмата/ полива цвете в саксия). В зависимост от наличните илюстративни материали, с които разполага детският учител, се предлага на децата да научат робота на разнообразни дейности, извършвани ежедневно в семейството и в детската градина. Упражнението се провежда така, че едно дете излиза на дъската и попълва блок-схемата с илюстрациите, а друго влиза в ролята на робота и изпълнява (или разказва как ще извърши) действията, като групата следи, дали алгоритъмът е в правилната последователност. Ако не е, роботът няма да се научи да изпълнява дадената дейност. Важно е подбраните примери да са за дейности, които се изпълняват в неизменен ред, например: засаждане на растение; измиване на чиния; поставяне на инжекция; правене на снимка; приготвяне на сандвич с масло и салам и т.н.
- Определяне на последователност от действия за осъществяване на позната дейност в блок-схема на линеен алгоритъм
Осъществяването на тази задача в предучилищна възраст е свързано с известни трудности. Първо, защото децата се затрудняват да опишат словесно еднозначна последователност от действия и второ, поради факта че дори и да го направят, не е възможно да запишат или нарисуват реда на стъпките. Ето защо в 5-6-годишните създават предимно алгоритми за движение, където могат да кодират алгоритъма със стрелки. Все пак по преценка на учителя може да им се предложи да опишат словесно поредността на действията за осъществяване на позната дейност. Учителят може да ги напише в отделни овали и след това под диктовката на групата да ги подреди в празна блок-схема. Изискванията към примерите са както в предходната задача. Подходящи са следните дейности: измиване на зъбите; пресичане на улицата; обаждане по телефона; закусване в детската градина; приготвяне за сън в детската градина; измиване на ръцете.
- Изпълнение на зададен линеен алгоритъм за движение
Децата се подготвят да създават алгоритми за движение, като първо се учат да изпълняват готови такива. Предлага им се да проверят в коя стая трябва да отиде роботът, като го придвижат съобразно посоките на стрелките.
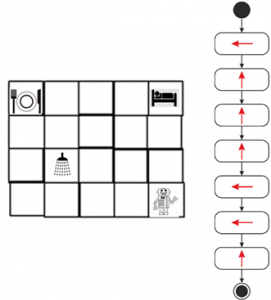
Фигура 5. Линеен алгоритъм „Къде ще стигне роботът?“
- Създаване на линеен алгоритъм за движение
Задачата е подобна на горната, но в случая е зададена крайната цел на движението, а децата трябва да запишат алгоритъма за достигането й със стрелки: „Да научим робота да кара кола. Трябва да я закара в гаража, без да преминава през препятствията. Запиши указанията за движението му със стрелки.“
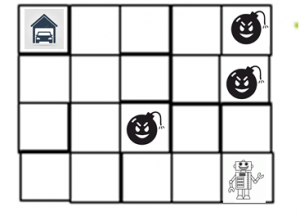
Фигура 6. Линеен алгоритъм „Роботът кара кола“
- Създаване на линеен алгоритъм за движение и последователност от действия (при конструиране)
Като усложнение за по-напредналите деца може да се комбинира алгоритъмът за движение с алгоритъм за построяване на обект по образец: „Да научим робота да строи. Запиши със стрелки пътя му, като спазваш последователността при построяването на къщата – първо се поставя правоъгълника за основа, после върху него две кубчета и накрая покрива.“ Отново се акцентира (а може и да се демонстрира с реален конструктор), че ако не се спазва точно дадената последователност, постройката няма да се получи.
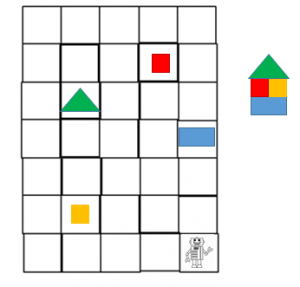
Фигура 7. Линеен алгоритъм „Роботът строи къща“
- Изпълнение на алгоритъм с цикъл
На децата се обяснява, че роботът може да се научи да изпълнява и действия, които се повтарят по няколко пъти. Както например в приказките героите могат да извършват многократно определени действия. Житената питка докато се търкаляла по пътечката няколко пъти срещала животни и това се повтаряло, докато стигнала до лиса. „Можем да направим схема за робота, която да му показва докога да повтаря някакви команди. За целта трябва да отговори на въпрос с „да“ или „не“. Ще ги покажем на схемата с ръчички – за „да“ – вдигнат палец; за „не“ – обърнат надолу палец. На блок-схемата въпросът се записва в ромб. От него излизат две стрелки. Ако отговорът е „да“, се тръгва по едната стрелка; ако е „не“ – по другата. В зависимост от отговора, роботът трябва да следва едното или другото разклонение на блок-схемата“. Предлага се децата да се разделят на два отбора и всеки от тях да излъчи свой представител – дете, което влиза в ролята на робот. Двата робота могат да се състезават кой по-дълго ще остане в цикъла. Цикълът се представя във вид на блок-схема на пода и избраните „роботи“ последователно преминават през нея. Друг вариант е участниците да движат фигурки на роботи в блок-схемата, изобразена на игрално поле. На фигура 8 победител е този, който остане по-дълго в цикъла.
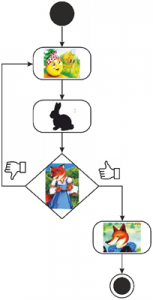
Фигура 8. Цикличен алгоритъм „Житената питка“
На фигура 9 победител е роботът, който събере повече яйца, т.е. изпълни повече цикли.
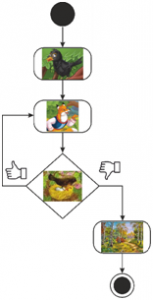
Фигура 9. „Косе Босе“
В зависимост от предложения сюжет, съревнованието може да е не кой ще остане по-дълго в блок-схемата, а кой ще излезе по-бързо от нея. На фигура 10. Победител е роботът, който по-бързо се потопи в златната вода на реката.
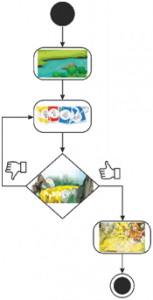
Фигура 10. „Златният робот“
- Изпълнение на разклонен алгоритъм
Обяснява се, че роботът може да изпълнява и по-сложни алгоритми. Ако е изпълнено дадено условие, се извършват едни действия; ако не е – други. Така на схемата ако отговорът на поставения в ромба въпрос е „да“, се следва едната стрелка; ако отговорът е „не“ се следва другата стрелка. Предлага се на децата да поставят картинките на блок-схемата, които показват какви действия трябва да изпълни роботът съобразно изпълнението или неизпълнението на даденото условие.
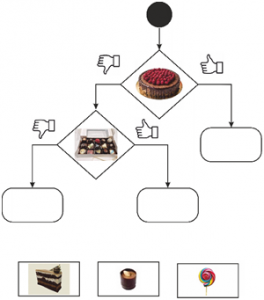
Фигура 11. Разклонен алгоритъм „Избор на десерт“
ЗАКЛЮЧЕНИЕ
Всеки тип задача от представената методическа последователност трябва да се предложи в няколко варианта, като се сменя сюжетното съдържание, с оглед развитие на алгоритмичните умения на децата. Целесъобразно е използването на блок-схеми на алгоритми при работата и по другите образователни направления. Препоръчително е блок-схемите да се оставят на разположение на децата, за да може тези от тях, които желаят да ги използват и играят с тях и след приключването на педагогическите ситуации. По думите на Г. Георгиева „обособяването на математически център, оборудван с дидактични материали и обвързан тематично с преподаването на математическото съдържание би стимулирало децата при свободната игра да се ангажират практически и по свое желание продължат работата по математика“ (Г. Георгиева, 2014, с. 170).
Използването на блок-схеми съответства на особеностите на детското мислене и обезпечава нагледност при развитието на алгоритмичното мислене. По този начин се полагат основите на дигиталната компетентност, която е важна за живот и успешна реализация в информационното общество.
ЛИТЕРАТУРА
- Георгиева, Г. (2014). Диференцираност в обучението по математика в смесена възрастова група в детската градина. Научни трудове на Русенския университет, 53 (6.2), 168-172.
- Гълъбова, Д. (2009). Теория и методика на формиране на елементарни математически представи у децата в детската градина. Велико Търново: Слово.
- Димитров, Д. , М. Касева. (2014). Формиране на понятие за алгоритъм и развитие на алгоритмичните умения у учениците. Личностно развитие на учениците в съвременното образование и общество, Благоевград, 7, 61-87.
- Касева, М. (2015). Развитие на алгоритмични умения на учениците от втори клас чрез информационни технологии. Автореферат на дисертационен труд за присъждане на ОНС „доктор“ от професионално направление 1.2. Педагогика, докторска програма „Начална училищна педагогика“. Благоевград: ЮЗУ „Неофит Рилски“.
- Пархоменко, С. (2020). Тетрадь Логика и программирование, 5-6 лет. Санкт-Петербург: Банда умников.
- Семадени, З. (1976). Съвременната математика при обучението на децата. София: Народна просвета.
- Утюмова, Е. (2016). Условия формирования алгоритмических умений у детей дошкольного возраста. Педагогическое образование в Росии, 3, 94-100.
REFERENCES
- Georgieva, G. (2014). Diferentsiranost v obuchenieto po matematika v smesena vazrastova grupa v detskata gradina. Nauchni trudove na Rusenskia universitet, Vol. 53 (6.2), 168-172.
- Galabova, D. (2009). Teoria i metodika na formirane na elementarni matematicheski predstavi u detsata v detskata gradina. Veliko Tarnovo: Slovo.
- Dimitrov, D. , M. Kaseva. (2014). Formirane na ponyatie za algoritam i razvitie na algoritmichnite umenia u uchenitsite. Lichnostno razvitie na uchenitsite v savremennoto obrazovanie i obshtestvo, Blagoevgrad, Vol.7, 61-87.
- Kaseva, M. (2015). Razvitie na algoritmichni umenia na uchenitsite ot vtori klas chrez informatsionni tehnologii. Avtoreferat na disertatsionen trud za prisazhdane na ONS „doktor“ ot profesionalno napravlenie 1.2. Pedagogika, doktorska programa „Nachalna uchilishtna pedagogika“. Blagoevgrad: YuZU „Neofit Rilski“.
- S. (2020). Tetrad Logika i programmirovanie. 5-6 let. Sankt-Peterburg: Banda umnikov.
- Semadeni, Z. (1976). Savremennata matematika pri obuchenieto na detsata. Sofia: Narodna prosveta.
- E. (2016). Usloviya formirovaniya algoritmicheskikh umeniy u detey doshkolnogo vozrasta. Pedagogicheskoe obrazovanie v Rosii, Vol.3. 94-100.
